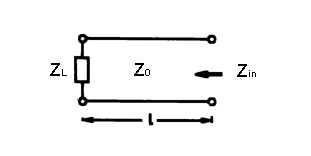
Transformation einer Impedanz ZL in eine Impedanz Zin durch eine Leitung mit der (komplexen) Impedanz Z0 der Länge l.
Bei der Simulation von (Vertikal-)Antennen sind als zwei entscheidende Faktoren die Leitfähigkeit und Dielektrizitätskonstante des Bodens bei Hochfrequenz einzugeben. Genau diese Werte sind aber bisher nur Schätzungen oder einfachste Karten für Lang- und Mittelwellensender. Angaben für den Kurzwellenbereich sind überhaupt nicht zu finden. Dabei sind die Bodeneigenschaften sehr von der Frequenz abhängig. Daher möchte ich diese Werte über einen längeren Zeitraum zusammen mit der Niederschlagsmenge und Temperatur selbst beobachten.
Mit dem gezeigten Verfahren lassen sich die Bodeneigenschaften leicht an mehreren Stellen für alle gewünschten Frequenzen messen. Die Messung bezieht sich natürlich nur auf die oberste Schicht, in der die Leitung eingebracht wird. Bei einem Felsboden mit 40cm Humus im Blumenbeet gemessen stellt diese Messung nicht den Durchschnitt der Umgebung dar! Mit Augenmaß sind aber durchaus sehr brauchbare Ergebnisse zu erzielen.
Letztendlich dienen diese Werte zum Vergleich zweier Groundplane-Antennen mit resonanten erhöht aufgebauten oder vergrabenen Radialen sowohl in der Simulation mit NEC4.1 sowie bei einer ausführlichen Messung.
Es wird eine Zweidrahtleitung in den Boden eingebracht und die Impedanz am oberen Ende vektoriell gemessen. Die Leitung im Boden ist am unteren Ende offen. Die Leitung transformiert die Impedanz des offenen unteren Endes in Abhängigkeit von ihren geometrischen Eigenschaften und den Eigenschaften des Mediums (Erdboden). Die allgemeine Leitungsgleichung wird benutzt um die relative Dielektrizitätskonstante εr und die spezifische Leitfähigkeit σ zu bestimmen.

Transformation einer Impedanz ZL in eine Impedanz Zin durch eine
Leitung mit der (komplexen) Impedanz Z0 der Länge l.
Es gilt
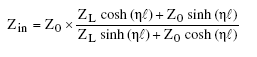 mit
mit
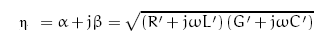
Da die Leitung am unteren Ende offen ist, wählen wir für ZL einen noch zu bestimmenden Wert, welchen den "Endeffekt" der Leitung berücksichtigt.
Hier lesen Sie ein Ansatz zur Näherung dieses Endeffekts der offenen Zweidrahtleitung.
Weiterhin gilt bei einer Zweidrahtleitung wie abgebildet
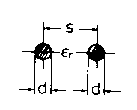
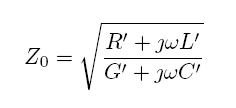
Die Leitungsbeläge bestimmen sich dabei zu:
C' = ε0 * εr * π / acosh(s/d)
L' = µ0 * µr / π * acosh(s/d) ; [1]
G' = σ * π / acosh(s/d)
R' = 1,66 * 10-7 * K1 * √f / d ;mit Vereinfachung nach [2] für diese dicken Leiter
---------------------
[1] µr bei Hochfrequenz (~1.0 im ganzen HF-Bereich, auch bei magnetischem Baustahl)
[2] Janzen, Gerd: Kurze Antennen : Entwurf u. Berechnung verkürzter Sende- und Empfangsantennen, 1986, ISBN 3-440-05469-1
| Leiter | K1 |
| Aluminium legiert | 1,3 - 2,0 |
| Kupfer | 1,0 |
| Messing | 1,9 - 2,3 |
| Zink | 1,9 |
| Stahl | 2,8 - 3,6 |
| rostfreier Stahl | 7,2 |

Mit dem neuen Vektor-Netzwerk-Analysator von DG8SAQ ist eine genaue Analyse für jeden Amateur möglich.

Alle zur Messung benötigten Teile.
Die mechanischen Abmessungen meiner Leitung sind d = 8,0 mm s = 48,0 mm l = 400 mm

Messung mit Laptop, Vektor-Netzwerk-Analysator von DG8SAQ und
Leitung im Boden.

Ende der Zweidrahtleitung im Boden mit Adapterstück und Koaxialkabel.
Die in den Boden einzubringende Leitung besteht hier aus zwei Eisenstangen mit 8mm Durchmesser und 40cm Länge. Die beiden Stangen haben an einem Ende ein Gewinde und ein Ende ist angespitzt, um das Eindrücken in den Erdboden zu erleichtern.
Eine der beiden Platten mit zwei Löchern wird auf den Boden gelegt und dient zu Stabilisierung des Abstandes der Stangen. Die andere Platte ist am oberen Ende mit Muttern verschraubt. Die Stangen werden dann so zusammen befestigt wie auf dem Bild gezeigt in den Erdboden gedrückt. Ist die Leitung ganz im Boden, werden beide Platten entfernt und das Adapterstück (hier mit N-Stecker) angeschraubt und die Messung vorgenommen. Für das Adapterstück sind zwei angepasste Kalibrierstandards angefertigt, damit eine SOL-Kalibrierung erfolgen kann. Mit den Platten lassen sich die Stangen auch wieder einzeln sehr gut aus dem Erdboden herausziehen.
Vergessen Sie nicht, über einen BalUn zwischen Ihrem Netzwerkanalysator und der symmetrischen Zweidrahtleitung zu denken. Oder Ihr Aufbau ist erdfrei und die Anschlussleitung sehr kurz wie bei mir.
Die Umrechnung der gemessenen Impedanz in die relative Dielektrizitätskonstante εr
und die spezifische Leitfähigkeit σ des Bodens erfolgt mit einer numerischen Lösung (Solver).
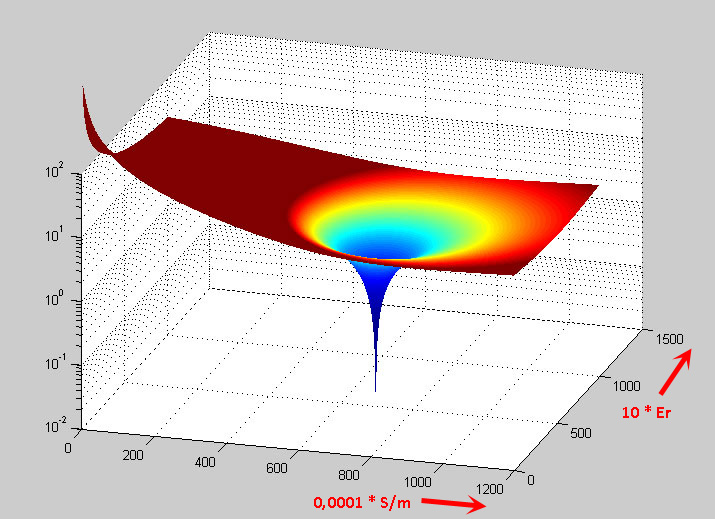
Bei der Lösung der Gleichung können sehr schöne Bilder anfallen. Im Bild ist die Abweichung der möglichen
Lösungen von der gesuchten Lösung dargestellt. Die X- und Y-Achsen spannen die Ebene aller möglichen Eigenschaften εr und σ.
Mit meinen selbst entwickelten Programm kann die Erdbodeneigenschaft berechnet werden:
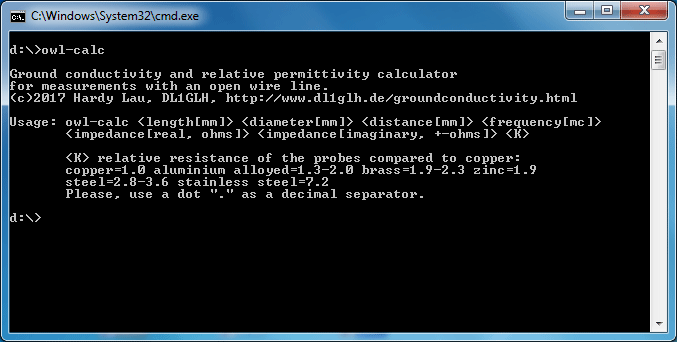
Aufruf des Programmes im Kommandofenster unter Windows ohne Parameter.
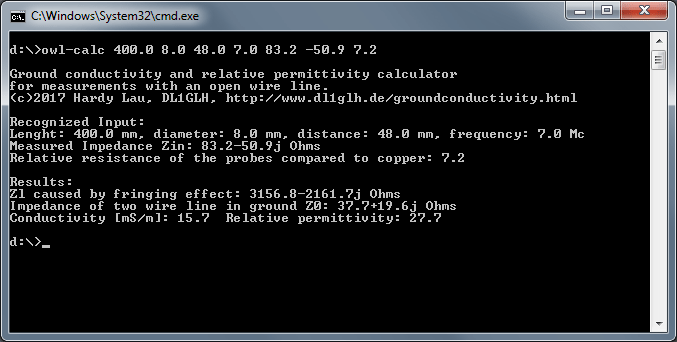
Aufruf mit den Parametern und die Ausgabe der berechneten Werte.
Das Programm owl-calc mit Quelltext (GPL V3) zur Offline Berechnung (für Microsoft Windows) zum herunterladen.
Die numerische Lösung ist sowohl in "C" (GCC) als auch in Matlab entwickelt.
Durch die allgemeine Leitungsgleichung sind alle mechanischen Abmessungen möglich, solange die Leitung elektrisch nicht länger als 1/2 λ ist. Die Berechnung ist keine Näherung sondern eine exakte Lösung. Die Abmessungen orientieren sich also an der möglichen Mechanik und der Präzision des Messgerätes.
Die Plausibilität der Umrechnung in die gewünschten Erdbodeneigenschaften wurde schon mehrfach erfolgreich überprüft. Bei einer hohen Leitfähigkeit erfolgt auch die Messung an der richtigen Tiefe im Erdboden, da die Strom-Eindringtiefe, wie in der einschlägigen Literatur beschrieben, schon sehr klein ist. Gegebenenfalls muss das Mittel aus mehreren Messungen im Umfeld der Antenne bis zu mehreren Lambdas Abstand genommen werden.